Connectomics - Topology

One part of the connectome research which I conduct concerns itself with the topology of human brain networks. While there has been a lot of theoretical work on this topic (see background section), we are still far away from identifying difference in brain topology, for example, due to disease.
Here, I describe some of my more theoretical work on identifying and characterizing these differences in different populations. Many of these methodologies are currently in development, however, here I describe the basic underlying principles without the math that surrounds them. For more detail, please see any of the selected publications, which are linked at the end of each section.
Heat kernels
In a connectome, i.e. a human brain network, regions are communicating with one another. Importantly, in contrast to common investigations, this information may not spread along the shortest paths in these networks. Instead, information may also utilize paths that "stop" at other regions in the brain, where it gets processed before it continues to the next region. Traditional analyses utilizes the shortest paths, however, by employing the heat kernel, we can incorporate information through all possible paths within the network. This is due to the fact that the heat kernel can be used to describe the spread of heat (or information) throughout a complex system.
The video above illustrates the principle of heat dissipation throughout a network. In the beginning, all of the heat is situated in the left node and edge, whereas there is no heat in the rest of the network (black edges). As time progresses, the heat spreads at different speads, depending on the strength of the connection between the nodes. However, brain networks are usually not as simple as the toy network here. Below you see an example of heat dissipation in a human connectome. Here, the same amount of heat has been placed at each of the nodes in the brain, which is why the diagonal of this network is white in the beginning and the rest black. Based on the through MRI estimated connectivity profile, the heat then starts to spread out throughout the network. To understand the full underlying principle, I recommend looking at our accompanying publication.
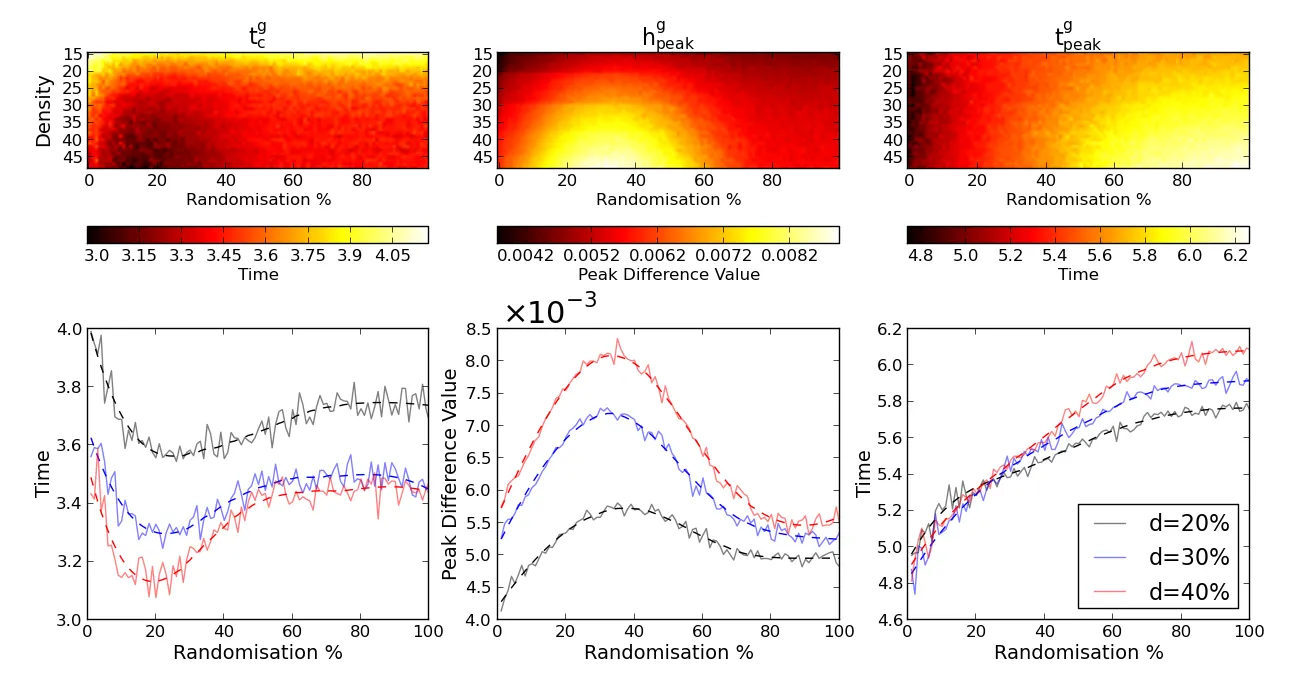
Using temporal heat kernel analysis, we looked, for example, at the time tc when the change in the heat between two time points "stabilizes", meaning that the change drops below a set threshold. In addition, we assessed the highest heat value hpeak that is observed in the network over all times, in addition to the time point tpeak at which it occurs.
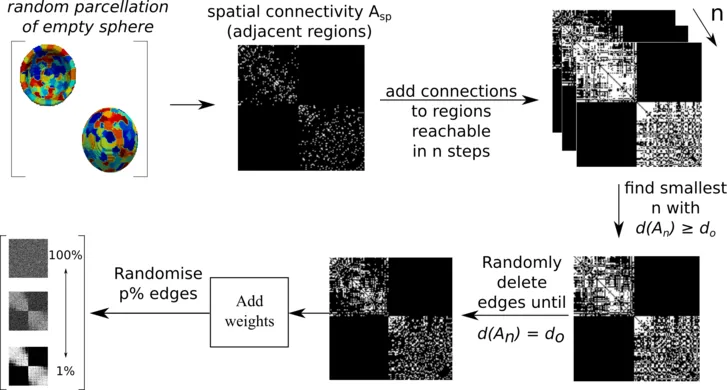
In order to confirm that we can utilize heat kernels to identify changes in network topology, we first created geometric synthetic networks. To do so, we created random parcellations on a half-sphere, and connected adjacent regions. Subsequently, we increased the network density to approximate the human connectome and then started to randomize the edges. This principle is outlined in the figure below.
By systematically changing the density of the networks, as well as the amount of randomization, we calculated these heat kernel measures for each synthetic networks. The figure below shows the heat kernel measures across al synthetic networks, as well as a 2D representation of three of the densities. Here, we observe three distinct areas in each of the measures. Furthermore, we have confirmed that the small-world networks are usually located within, e.g. the dark area in the intrinsic time constant (tc). This follows the intuition that small-world networks need the least amount to stabilize the information (heat) transport while transporting the maximum information.
Based on this principle, we were able to predict the two-year motor outcome of premature babies, to identify differences in peripheral subnetworks in children with autism, to distinguish comatose cardiac arrest patients waking up from those that will not, as well as to predict the benefit of fluid intelligence training. This large array of applications and capacity to differentiate between groups of patients and participants is just to demonstrate the potential that heat kernel analysis holds in analysing the human connectome.
Subnetworks
Modularity, or how we can divide the human connectome into smaller units, or subnetworks, has been a keen interest of researchers. This also results from the idea that some areas of processing is focused on dedicated areas of the brain. While recent research suggests that typical processing may be more distributed than we initially thought, subnetwork analysis can still help us identify differences between populations.
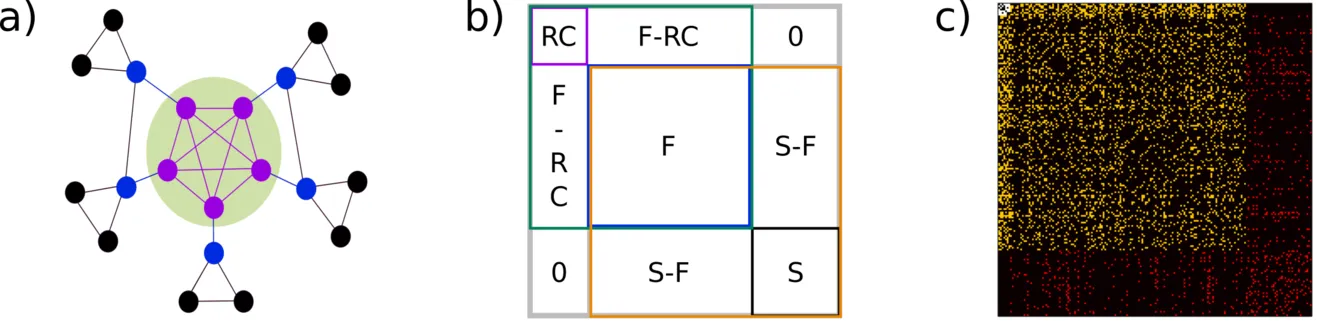
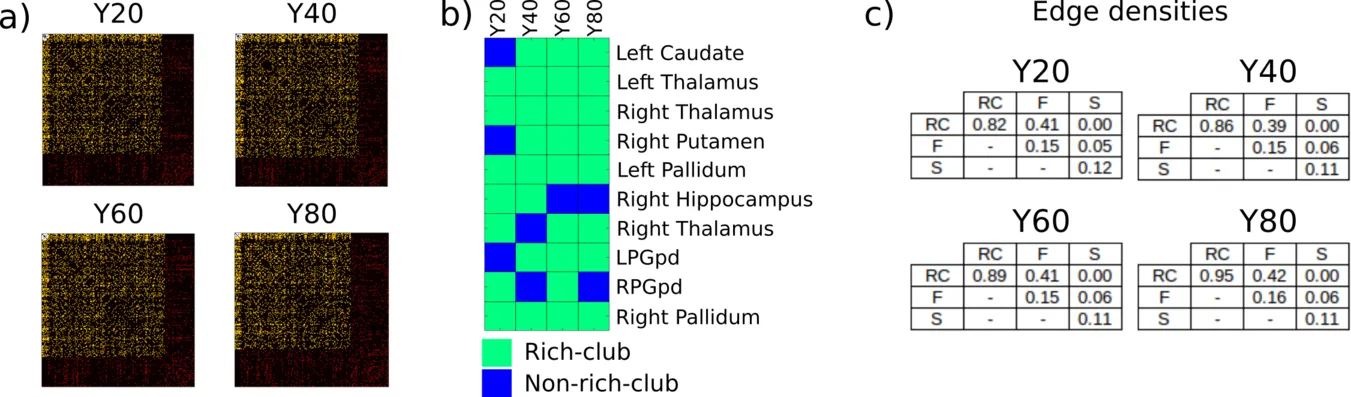
While there are many ways to subdivide the human brain, a principle that received massive attention is the rich-club (see background section). The set of regions that comprise the rich-club can be seen as a backbone of information transport. Subsequently we can divide the brain into subnetworks consisting of the rich-club (RC), the regions that are directly connected to the rich-club (Feeders; F), and the remaining regions (Seeders; S). This principle is illustrated in the figure below in a toy model (a), based on a connectivity matrix (b), and a real example from a human connectome (c).
In one of our works on the age dependent changes of subnetworks, we utilized this definition of subnetworks in a lifespan cohort of a healhty population. To allow consistent subnetwork definitions within age groups, we created group connectomes, the average connectome. Even in the analysis of the group connectomes, as shown in the figure below, demonstrated differences between age groups in the group connectomes (a-c), while the definition of the subnetworks remained relatively stable (b).
In addition to investigating the subnetwork differences with age, we also investigated topological differences in these subnetworks within a cohort of children with autism (Heat kernels with functional connectomes reveal atypical energy transport in peripheral subnetworks in autism). In this investigation we utilized the heat kernel framework on each of the subnetworks, which helped us to identify that the main differences are found within the peripheral subnetworks (seeders). This result highlights that it might not be the entire connectivity profile which is affected by a disease, but subnetworks, which may result in the symptoms that are observed.
Network dependency index
While we talked about subnetwork analysis using the rich-club analysis in the previous section, it is important to note that using rich-clubs is not the only way to define subnetworks. Importantly, as part of the rich-club analysis, one needs to select a relatively arbitrary threshold (wihtin bounds of course) which significantly impacts the number of regions belonging to the rich-club.
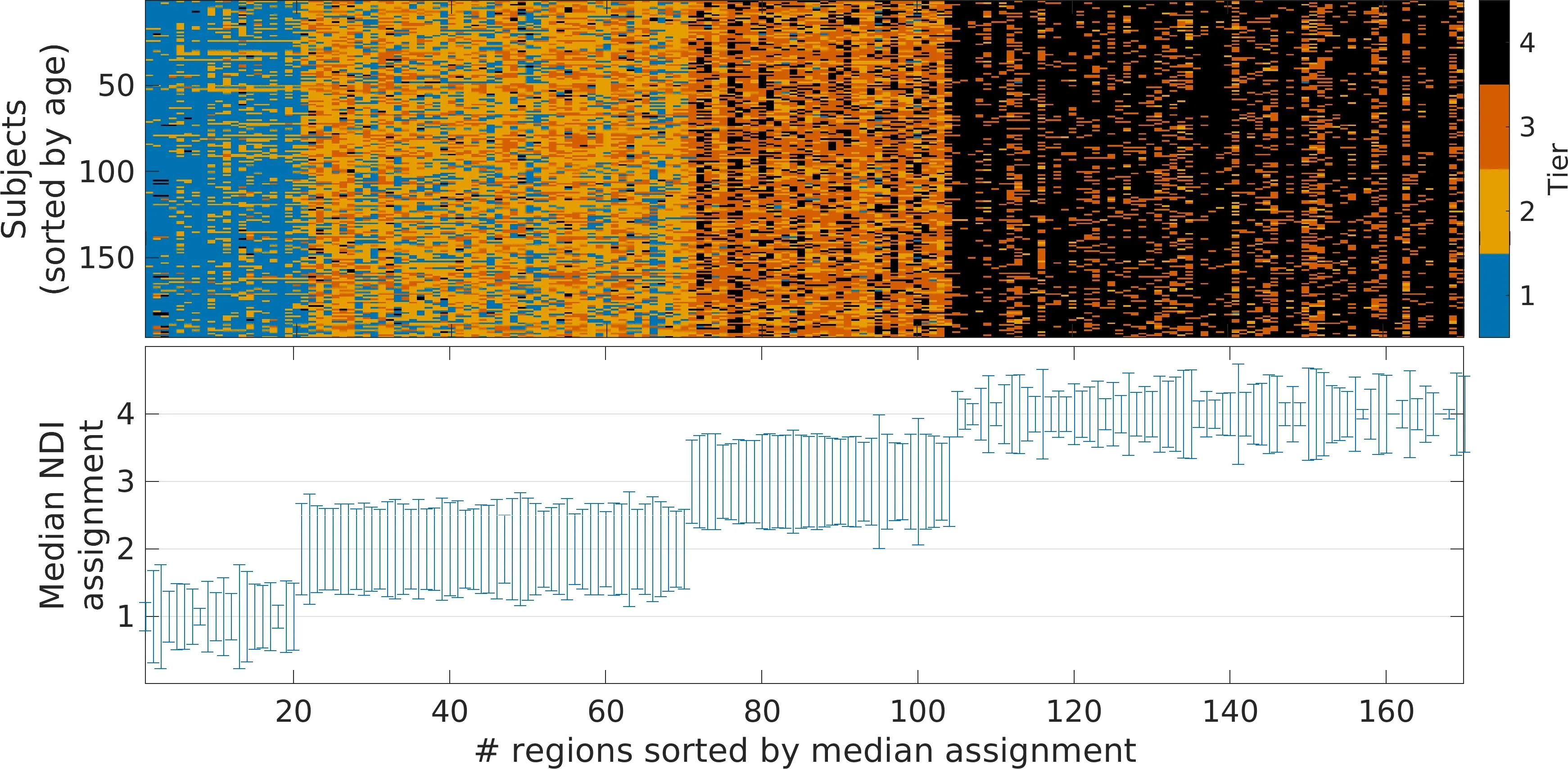
The rich-club is assumed to comprise the nodes that are of key importance for information transport within and generally the efficancy of the network. In 2018, Woldeyohannes and Jiang proposed a different metric of identifying regions that are integral for network efficiency - the network dependency index. While not initially designed to identify subnetworks, we extended the NDI metric into a framework which is able to consistently identify four distinct subnetworks in the human connectome ("Network Structural Dependency in the Human Connectome Across the Life-Span"). Importantly, this subnetwork definition is data driven, which means it is possible to do without any manually chosen parameters or thresholds, and even shows higher consistency across age groups compared with those defined based on the rich-club.
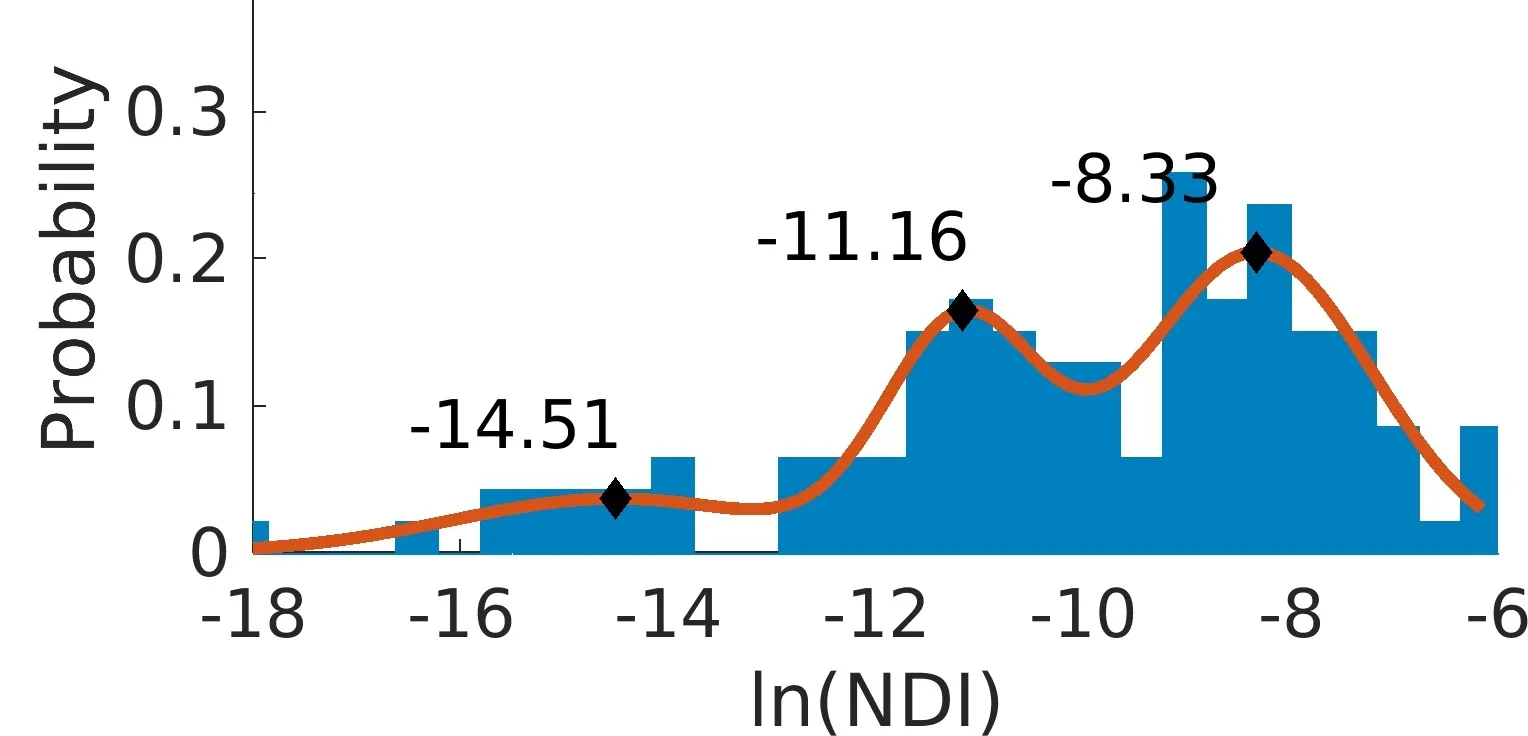
In very simple words, the network dependency index (NDI) quantifies the drop of efficiency, if a particular region in the brain would be removed or damaged, for example, as a result of a stroke. Once the NDI for each region in the connectome is calculated, we plot the histogram of the log-transformed values greater than 0, resulting in three distinct Gaussians, as illustrated below. Each Gaussian, together with the regions having an NDI of 0, make up the four subnetworks, or Tiers, of the connectome.
Comparing the regions of the rich-club with the regions deemed most important in the NDI framework, we can see that there is a good agreement between both methodologies. However, these regions are more consistently identified across age groups, when utilizing the NDI framework. This may be a direct result of aiming to utilize the same threshold in the rich-club methodology across groups in order to make the analysis more uniform, and highlights further that user defined parameters or thresholds can lead to drastically different results.
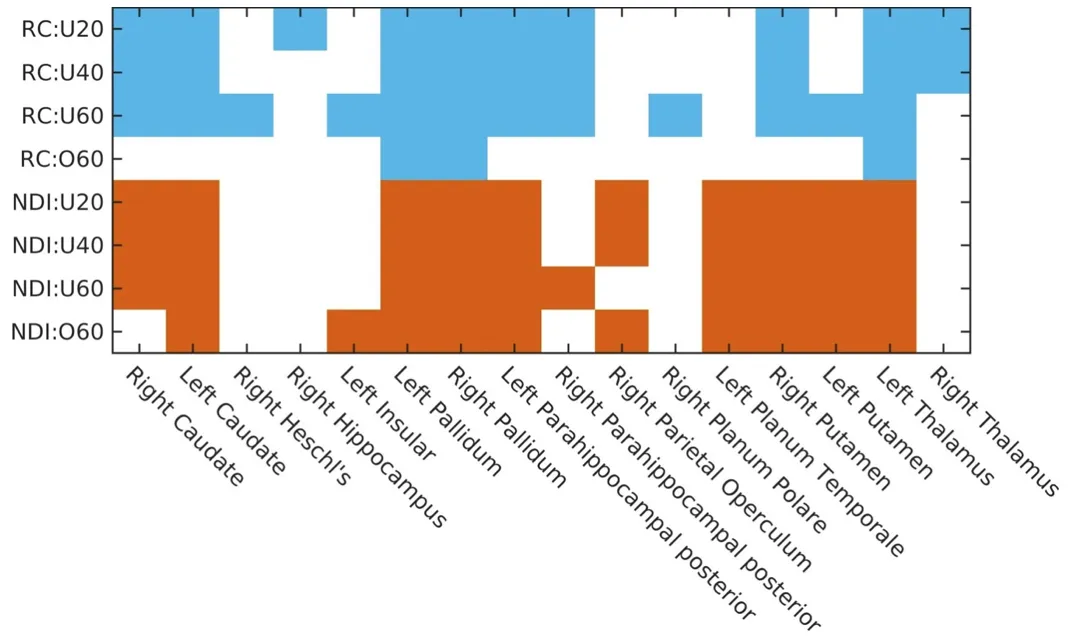
We can further see the consistency when applying the NDI framework to each connectome within our healthy cohort individually (see figure below). While we observe some variations, which may be a result of individual differences or due to measurement noise in creating the connectome, the overall assignment of each region (enumerated due to space limitations) largely follows the same trend across all participants.